Заголовок в New York Post гласит: “Шанс 1 к 331 миллиарду: одни и те же номера нью-йоркской лотереи разыгрываются дважды за один день”. Звучит впечатляюще, но проблема в том, что это совершенно неверно. Что действительно так, так это то, что одни и те же пять номеров – 18, 21, 30, 35 и 36 – были разыграны в нью-йоркской лотерее Take Five как в дневном, так и в вечернем розыгрышах в четверг, 27 октября. В “Пост” сообщается, что “эксперты” (неназванные) сообщили им, что вероятность того, что это произойдет, составляет 1 к 331 миллиарду.
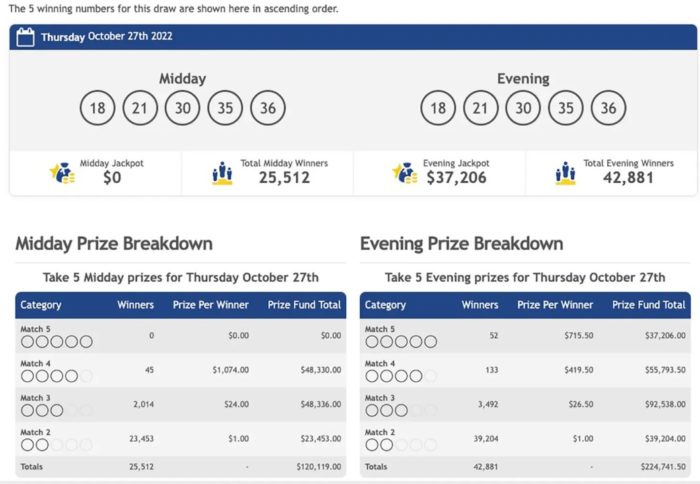
В “Пост” это назвали “лотерейным чудом”, но на самом деле это классический пример того, что не без оснований называют “лотерейной ошибкой”. Шансы на выигрыш в лотерее Take Five с одним билетом в любой конкретной игре равны 1 к 575 757. Эксперты The Post воспользовались калькулятором и умножили эти шансы на себя, получив 331 496 123 049. (Поэтому, по их мнению, экспертом является любой, у кого есть калькулятор.) Но это шансы на то, что эти пять чисел выпадут в двух розыгрышах подряд, а не шансы на то, что какие–либо пять чисел повторятся. Вероятность того, что любые пять чисел повторятся, равна 1 к 575 757 – вероятность того, что вечерние числа совпадут с полуденными (какими бы ни были эти полуденные числа). Эта лотерея проводится каждый день, так что за последние 10 лет было 3650 возможностей для того, чтобы это произошло. Вероятность того, что такое совпадение произойдет в каждом десятилетии, приближается к 1 из 157.
Но вероятность того, что такое совпадение произойдет по разным причинам, еще выше. Во-первых, в мире существует около 180 лотерей, в том числе 46 только в США. Более того, мы определяем критерии совпадения результатов лотереи постфактум. Что, если одинаковые числа выпадут дважды подряд, но не дважды в один и тот же день (скажем, при вечернем розыгрыше и на следующее утро). В “Посте” все равно будут ошибочно считать, что это чудо составляет 1 к 331 миллиарду. Это удваивает шансы, поскольку теперь и утренний, и вечерний розыгрыши могут совпадать с предыдущим (1 к 78 за десятилетие).
Однако люди считают удивительным совпадением, если одинаковые цифры выпадают почти одновременно, даже с разницей в несколько дней. В 2009 году в болгарской лотерее за одну неделю выпали те же числа. Это вызвало такую же реакцию, что и результаты лотереи в Нью-Йорке. Это значительно повышает вероятность выигрыша, поскольку теперь каждую последовательность чисел можно сравнить с любой другой последовательностью чисел в течение нескольких дней. За одну неделю лотереи было проведено пять розыгрышей, то есть 14 наборов чисел и 91 возможное сравнение (с использованием формулы k(k-1)/2).
Существуют и другие типы лотерейных совпадений, например, один и тот же человек выигрывает в лотерею дважды (даже с разными номерами). Когда это повторится, многие средства массовой информации допустят лотерейную ошибку и сообщат о неверных коэффициентах. Шансы на то, что этот конкретный человек выиграет в эту конкретную лотерею, купив два отдельных билета, могут быть астрономическими, но шансы на то, что кто-то выиграет в любую лотерею дважды, купив несколько билетов, довольно высоки. Какие-то лотерейные совпадения должны происходить регулярно, и они происходят примерно с той частотой, которую предсказывает правильная статистика.
Мы можем применить принцип лотерейной ошибки к вещам, не связанным с лотереей. Мы склонны замечать закономерности, которые бросаются в глаза, например, любое случайное совпадение фактов или происшествий. Тогда мы поражаемся невероятно низким шансам на то, что произойдет именно это совпадение. Но, опять же, мы должны учитывать вероятность любого совпадения. Вы мечтаете о ком-то, с кем не виделись много лет, и он звонит на следующий день. Должно быть, это экстрасенсорные способности – или просто предсказуемое стечение случайных событий в вашей жизни. Люди склонны недооценивать возможность такого стечения обстоятельств, потому что они недооценивают количество переменных факторов.
Предположим, что в среднем за неделю с вами происходит 100 определенных событий (просто чтобы использовать репрезентативное число – реальное число, скорее всего, намного больше). Это будет 4950 возможностей для того, чтобы любые два из этих событий каким–то образом совпали – каждую неделю. Мы также используем нечеткие критерии для определения того, что является выравниванием, обычно определяя критерии постфактум. Это справедливо для всех почти 8 миллиардов человек на планете (7,98 – почти достигли).
Количество возможностей для крайне маловероятного выравнивания столь же велико. Очевидно, что странные совпадения, в совокупности, должны происходить постоянно, так что неудивительно, что они случаются.
